Area of circle, formula and illustrated lesson: how to calculate the area of a circle

Formula for Area of circle

The formula to find a circle's area π (radius)2 usually expressed as π⋅r2 where r is the radius of a circle.

Diagram 1

Area of Circle Concept

The area of a circle is all the space inside a circle's circumference. In diagram 1, the area of the circle is indicated by the blue color.

The area is not actually part of the circle. Remember a circle is just a locus of points. The area is enclosed inside that locus of points.

Area of Circle SAT Prep Video

What is the area of the circle in the picture?

Round your answer to the nearest tenth.

Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (22')^2 \\ A = \pi \cdot 484 \\ A = 1520.53084433746 \text{ square feet} \\ \\ Area = \boxed{1520.5} \\ \text {Rounded to nearest tenth} $$

What is this circle's area?

Round your answer to the nearest tenth.

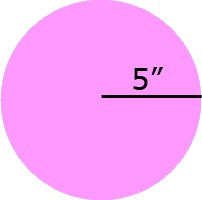
Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (5")^2 \\ A = \pi \cdot 25 \text{ square inches} \\ A = 78.53981633974483 \text{ square inches} \\ A = 78.5 \\ \text{ square inches, rounded to nearest tenth} $$

What is the area of a circle with a radius of 7 centimeters?

Round your answer to the nearest hundredth.

Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (7 \text{ centimeters})^2 \\ A = 153.93804002589985 \text{ square centimeters} \\ \boxed {A = 153.94} \\ \text{ square centimeters, rounded to nearest hundredth} $$

What is the radius of a circle if its area is 120 in2? (Round your answer to the nearest hundredth of an inch)

Use the area formula ... but this time solve the radius.

$$ A = \pi r^2 \\ 120 = \pi r^2 \\ \frac{120}{\pi} = r^2 \\ 38.197 = r^2 \\ \sqrt{38.197} = r \\ \boxed {r=6.18 \text{ inches}} $$

What is the diameter of a circle if its area is 360 in2?

(Round your answer to the nearest hundredth of an inch)

A circle has a diameter of 12 inches. What is its area in terms of π.

(Need a hint)

Remember: The formula for the area of a circle is based on the circle's radius not its diameter.

Divide Diameter in half to calculate radius:

Radius = $$ \frac{diameter}{2} = \frac{12}{2}= 6 $$.

Use area formula:

$$ A= \pi \cdot r^2 \\ A = \pi \cdot 6^2 \\ A = 36 \pi $$

If a circle's radius is doubled, then how much did its area increase?

Since the formula for the area of a circle squares the radius, the area of the larger circle is always 4 (or 22) times the smaller circle. Think about it: You are doubling a number (which means ×2) and then squaring this (ie squaring 2) -- which leads to a new area that is four times the smaller one.

You can see this relationship is true if you pick some actual values for the radius of a circle.

For instance, let's make the original radius = 3 .

$$ A_{larger} = \color{red}{4} \cdot A_{smaller} \\ A_{larger} = \color{red}{4} \cdot 9\pi \\ A_{larger} = 36 \pi $$

This relationship holds true no matter what radius you pick.

Let's make the original radius = 5.

$$ A_{larger} = \color{red}{4} \cdot A_{smaller} \\ A_{larger} = \color{red}{4} \cdot 25\pi \\ A_{larger} = 100 \pi $$