Satz des Thales

发布时间：2025-08-28 02:42

Definition

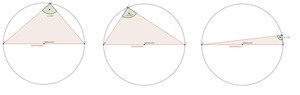
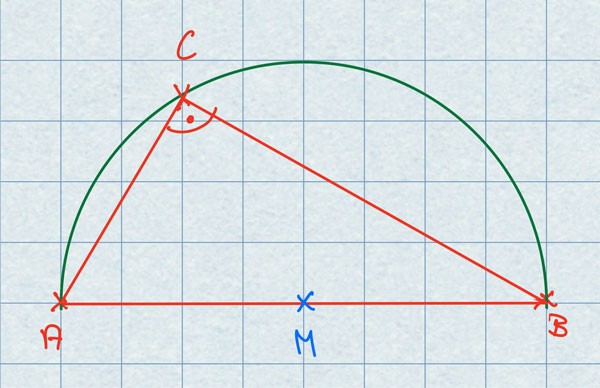
Der Satz des Thales ist einer der ältesten Sätze der Mathematik. Er besagt, dass alle Winkel in einem Halbkreisbogen rechtwinklig sind. Genau gesagt bedeutet das: Ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis) und einem weiteren Punkt dieses Halbkreises, ergibt immer ein rechtwinkliges Dreieck. Schauen wir uns dies an einer Skizze an.

satz-des-thales

Methode

Wie du siehst, entsteht, egal wohin du den Punkt D bewegst, immer ein rechtwinkliges Dreieck. Versuche dies einmal selbst mit dem Interaktiven Arbeitsblatt aus.

Bitte Box anklicken, um GeoGebra zu laden.

Was ist der Thaleskreis?

Der Thaleskreis ist eigentlich nichts anderes als ein Halbkreis, der durch den Durchmesser getrennt wird. Da der rechte Winkel immer gegenüber von dem Durchmesser ist, ist dieser immer die Hypotenuse des gebildeten rechtwinkligen Dreiecks.

Beweis des Thalessatzes

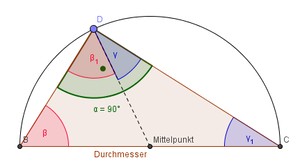
satz-des-thales-beweis

Abbildung Skizze Beweis Thalessatz

Vom Mittelpunkt zum Punkt D ziehen wir eine Hilfslinie und haben nun drei Dreiecke:

Dreieck: Eckpunkte B, C und DDreieck: Eckpunkte B, D und MittelpunktDreieck: Eckpunkte C, D und Mittelpunkt

Schauen wir uns nun die Dreiecke an. Unser Ziel ist es zu beweisen, dass \alpha = 90 ^\circ ist.
Schauen wir uns das große Dreieck BCD mit der Linie vom Mittelpunkt zum Punkt D an. Wir sehen, dass durch die Linie zwei gleichschenklige Dreiecke gebildet werden. Die drei Schenkel sind alle so groß wie der Radius. Aus diesem Grund sind die Winkel \beta und \beta_1 gleich groß und auch \gamma und \gamma_1.

Merke

Die Innenwinkelsumme eines Dreiecks beträgt immer 180 ^\circ!

Wenden wir die Regel der Größe der Innensummen auf unsere Aufgabe an. Dann ist also \alpha+\beta+\gamma_1 = 180^\circ.

Da \textcolor{red}{\alpha = \beta_1 + \gamma} können wir dies in die obere Formel einsetzten, dann erhalten wir:

\textcolor{red}{\alpha}+\beta+\gamma_1 = \textcolor{red}{\beta_1 + \gamma} +\beta+\gamma_1 = 180^\circ

Da \beta und \beta_1, \gamma und \gamma_1 den gleichen Betrag haben, können wir dies weiter umformen in:

2\cdot (\beta+ \gamma) = 180^\circ |:2

\beta + \gamma = 90^\circ

Da die Winkel \beta und \gamma zusammen den Winkel \alpha ergeben, können wir nun sagen, dass \alpha=90^\circ.

\textcolor{red}{\alpha = \beta + \gamma}

\alpha = 90^\circ

Damit haben wir schon bewiesen, dass \alpha immer 90^\circ groß sein muss.

Beispielaufgabe - rechtwinkliges Dreieck zeichnen

In den folgenden Beispielaufgaben zeigen wir die Schritt für Schritt, wie du den Satz des Thales nutzen kannst. Anschließend kannst du dich selbst überprüfen. Los geht's!

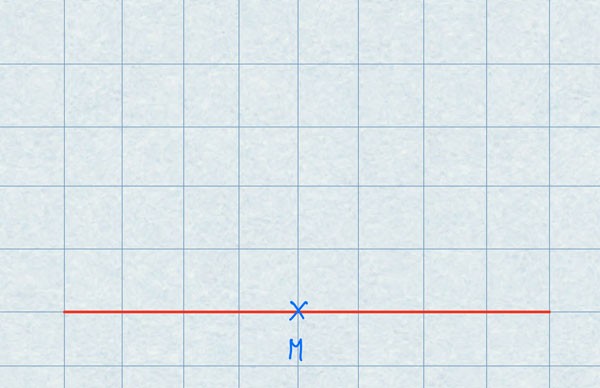
Zeichne eine farbige Linie mit einer Länge von 8 cm. Markiere anschließend den Mittelpunkt dieser Linie.

Satz des Thales: Mittelpunkt einzeichnen

Nimm nun deinen Zirkel zur Hand und stelle ihn auf 4 cm.

Steche den Zirkel in den Mittelpunkt und zeichne vom Anfang der farbigen Linie bis zum Ende.

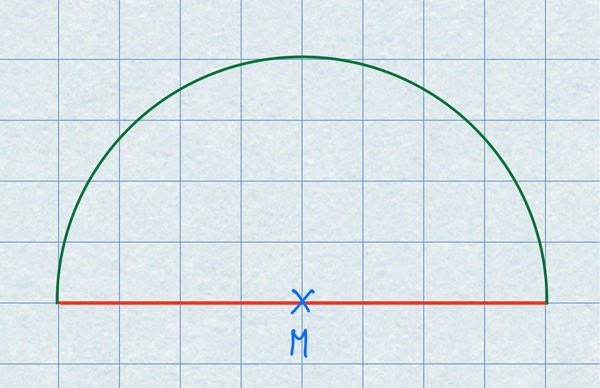
Satz des Thales: Halbkreis einzeichnen

Jetzt hast du oberhalb der Linie einen Halbkreis.

Benenne als nächstes Anfang und Ende der Linie mit A und B. Markiere anschließend irgendwo auf dem Halbkreis einen Punkt C. Verbinde A mit C und B mit C.

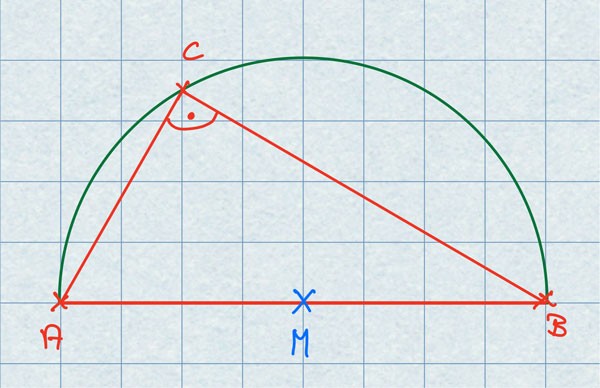
Satz des Thales: Punkt C einzeichnen

Bei dem Dreieck ABC handelt es sich um ein rechtwinkliges Dreieck. Der rechte Winkel ist bei C.

Nun markiere auf dem Halbkreis einen anderen Punkt D und verbinde wie oben mit A und B.

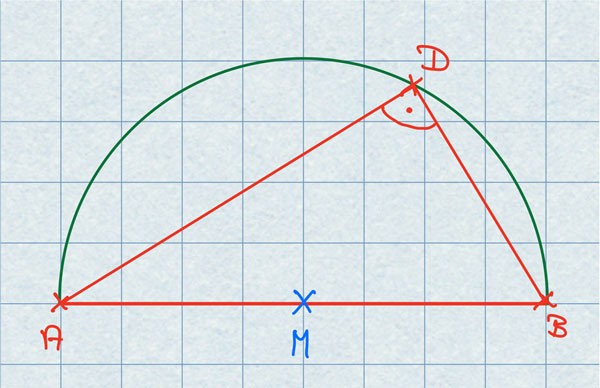
Satz des Thales: Punkt D einzeichnen

Das neue Dreieck ABC ist auch ein rechtwinkliges Dreieck.

Beispielaufgabe - Winkel messen und berechnen

Zeichne ein rechtwinkliges Dreieck. Miss dann den Winkel bei A:
\alpha =

Berechne den Winkel bei B:
\beta = 90^\circ - \alpha =

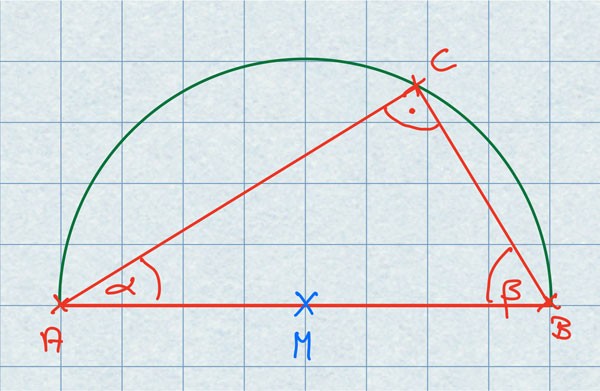
Satz des Thales: Winkel messen und berechnen

Ergebnis: Die Werte in dieser Zeichnung lauten \alpha = 32^\circ und \beta = 90^\circ - 32^\circ = 58^\circ

Beispielaufgabe - Überprüfung, ob ein Dreieck einen rechten Winkel hat

Miss alle Seiten und wähle die längste Seite. Markiere auf der längsten Seite den Mittelpunkt M. Steche den Zirkel in diesen Mittelpunkt. Zeichne einen Halbkreis von A nach B.

Falls C nicht auf dem Halbkreis liegt, so ist das Dreieck auch nicht rechtwinklig.

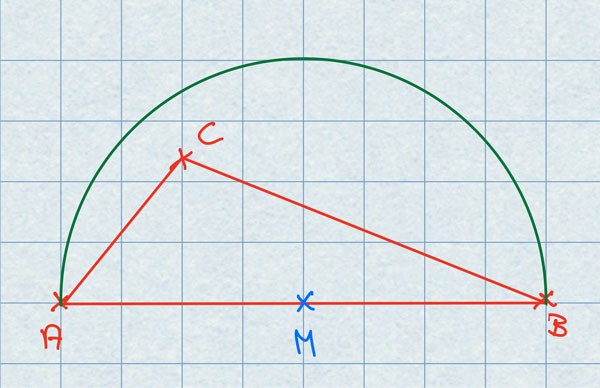
Satz des Thales: Winkel prüfen

Falls C auf dem Halbkreis liegt, so ist das Dreieck rechtwinklig.

Thalessatz: Winkel prüfen

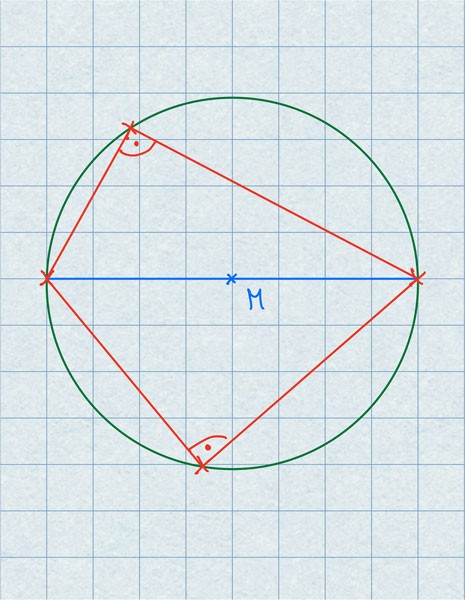
Beispielaufgabe - Viereck mit zwei rechten Winkeln

Zeichne einen Kreis und einen Durchmesser. Markiere zwei Punkte auf dem Kreis. Verbinde die vier Punkte auf dem Kreis zu einem Viereck. Dieses Viereck hat zwei Winkel, die rechtwinklig sind.

Thalessatz: Viereck mit zwei rechten Winkeln