Satz des Thales: Erklärung und Beispiele

Geschrieben von: Dennis Rudolph
Montag, 04. Juni 2018 um 17:19 Uhr

Was man unter dem Satz des Thales (und seiner Umkehrung) versteht, lernt ihr hier. Dies sehen wir uns an:

Eine Erklärung wozu man den Satz des Thales braucht. Beispiele zur Nutzung des Thaleskreises. Aufgaben / Übungen damit ihr dies selbst üben könnt.Ein Video zu diesem ThemaEin Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Wer von einem Dreieck noch gar keine Ahnung hat, kann gerne erst noch in die Dreieck Übersicht reinsehen.

Anzeigen:

Satz des Thales einfach erklärt

Starten wir mit einer einfachen Erklärung zum Satz des Thales. Dazu soll erst einmal kurz erklärt werden, wie man einen Thaleskreis konstruiert. Um dies zu tun, zeichnen wir mit Geodreieck oder Lineal erst einmal eine Linie mit einer Länge von 8 cm.

Wir markieren den Mittelpunkt dieser Linie, hier mit M bezeichnet.

Die Linie ist jetzt 8 cm lang und wir haben den Mittelpunkt. Als nächstes brauchen wir einen Zirkel. Diesen stellen wir auf 4 cm ein. Wir stechen bei M ein und die Bleistiftspitze erreicht das Ende der roten Linie. Wir zeichnen damit einen Halbkreis oberhalb der roten Linie.

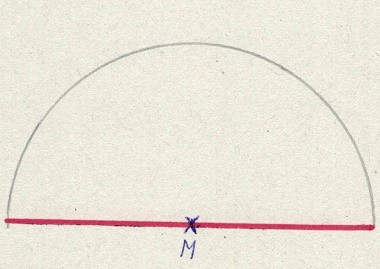
Jetzt haben wir einen Thaleskreis. Was fangen wir damit an? Wir zeichnen ein Dreieck ein, wobei die rote Linie ein Teil des Dreiecks ist und wir nehmen irgend einen Punkt auf dem Halbkreis. Dabei entsteht oben immer ein rechter Winkel!

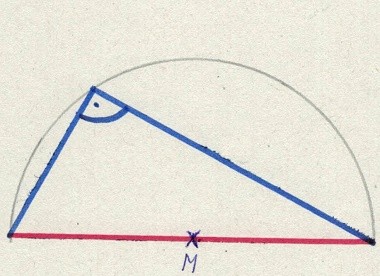
Dies auch noch einmal mit einem weiteren Dreieck:

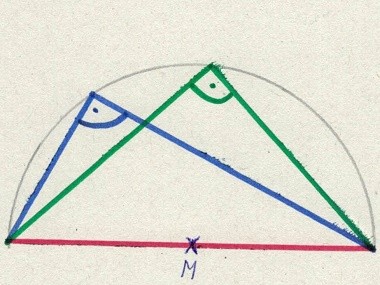
Was lernen wir daraus?

Hinweis:

Wird ein Halbkreis über der längsten Strecke gezeichnet und die Enden der Strecke mit einem Punkt auf dem Halbkreis verbunden, dann entsteht dabei immer ein rechter Winkel.

Man kann den Satz des Thales auch umkehren:

Hinweis:

Der Mittelpunkt des Umkreises des rechtwinkligen Dreiecks liegt in der Mitte der Hypotenuse - also der längsten Seite des Dreiecks - die dem rechten Winkel gegenüberliegt.

Anzeige:

Anzeigen:

Beispiele Satz des Thales

In diesem Abschnitt sehen wir uns zwei Beispiele zum Satz des Thales ein.

Beispiel 1: Rechtwinkliges Dreieck erzeugen

Mit Hilfe vom Satz des Thales soll ein rechtwinkliges Dreieck erzeugt werden. Die längste Seite soll dabei 6 cm lang sein und eine weitere Seite soll 4 cm lang werden. Zeichne das Ergebnis.

Lösung:

Wir zeichnen eine 6 cm lange Linie (in rot).Wir markieren den Mittelpunkt der Linie (und schreiben M daran).Wir zeichnen mit einem Zirkel einen Halbkreis.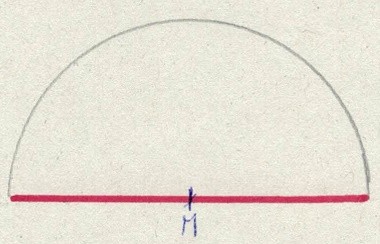

Jetzt soll noch eine Seite 4 cm lang werden.

Dies erreichen wir, indem wir einen Zirkel auf 4 cm einstellen.Wir stechen in einen der Eckpunkte ein (zum Beispiel den links unten) und markieren damit im Abstand von 4 cm einen Punkt auf dem Thaleskreis.Diesen verbinden wir mit den Eckpunkten um ein rechtwinkliges Dreieck zu erzeugen.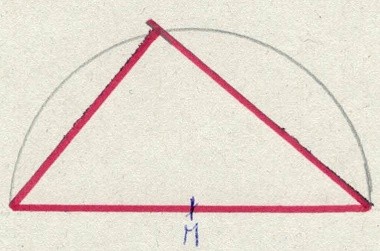

Beispiel 2: Ist das Dreieck rechtwinklig?

Wir haben dieses Dreieck. Zeige mit dem Thaleskreis, dass es einen rechten Winkel hat.

Lösung:

Die längste Seite ist die unten und liegt gegenüber von etwas, was ein rechter Winkel sein könnte. Wir halbieren daher die Strecke und zeichnen den Punkt M ein. Über diesem zeichnen wir einen Thaleskreis. Da der Eckpunkt auf dem Kreis liegt, haben wir hier einen rechten Winkel.

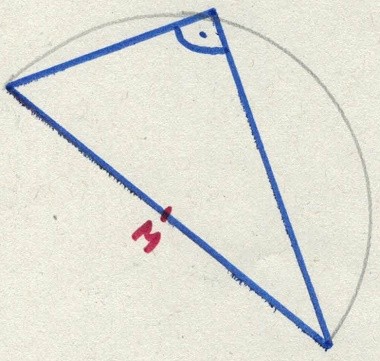
Fazit: Wir haben einen rechten Winkel nachgewiesen.

Anzeigen:

Aufgaben / Übungen Satz des Thales

Anzeigen:

Video Satz des Thales

Erklärung und Beispiel

Diese Inhalte werden besprochen:

Der Satz des Thales wird besprochen.Dabei wird ein Thaleskreis gezeichnet.Mit dessen Hilfe werden rechtwinklige Dreiecke erzeugt.Allgemeine Erklärungen zum Thema.

Nächstes Video »

Fragen mit Antworten zum Thaleskreis

Anzeigen:

Neue Artikel

Raute ▷ Formeln, Eigenschaften und BeispieleSachaufgaben Klasse 5 Mathematik AufgabenSachaufgaben Mathe: Klasse 5Worte in Zahlen Aufgaben (Übungen)Worte in Zahlen umwandelnTeilerfremdheit (Mathematik)Hohlmaße umrechnenHundertertafel GrundschuleQuersumme berechnen und TeilbarkeitQuadratzahlen berechnen (mit Liste)

Hat dieser Artikel dir geholfen?

网址：Satz des Thales: Erklärung und Beispiele https://klqsh.com/news/view/192130

相关内容

Satz des Thales und Thaleskreis Erklärung
Wann wird „obsolet“ selbst ungebräuchlich und überflüssig?
Bedeutung von „obsolet“ einfach erklärt
Bewerten ᐅ Synonyme, Bedeutung, Definition
Paketmarke: Einfach von zuhause aus frankieren
bewerten – Schreibung, Definition, Bedeutung, Etymologie, Synonyme, Beispiele
Was bedeutet “obsolet”? Bedeutung, Definition, Erklärung
obsolet – Schreibung, Definition, Bedeutung, Etymologie, Synonyme, Beispiele
ATX erklärt: Überblick und Werte
Gedichte und Reime finden und selber schreiben

随便看看